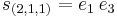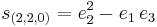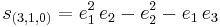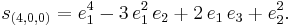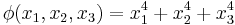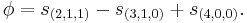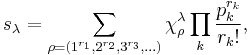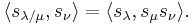Schur polynomial
In mathematics, Schur polynomials, named after Issai Schur, are certain symmetric polynomials in n variables, indexed by partitions, that generalize the elementary symmetric polynomials and the complete homogeneous symmetric polynomials. In representation theory they are the characters of irreducible representations of the general linear groups. The Schur polynomials form a linear basis for the space of all symmetric polynomials. Any product of Schur functions can be written as a linear combination of Schur polynomials with non-negative integral coefficients; the values of these coefficients is given combinatorially by the Littlewood-Richardson rule. More generally, skew Schur polynomials are associated with pairs of partitions and have similar properties to Schur polynomials.
Contents |
Definition
Schur polynomials correspond to integer partitions. Given a partition
(where each 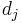 is a non-negative integer), the following functions are alternating polynomials (in other words they change sign under any transposition of the variables):
is a non-negative integer), the following functions are alternating polynomials (in other words they change sign under any transposition of the variables):
Since they are alternating, they are all divisible by the Vandermonde determinant:
The Schur polynomials are defined as the ratio:
This is a symmetric function because the numerator and denominator are both alternating, and a polynomial since all alternating polynomials are divisible by the Vandermonde determinant.
Properties
The degree d Schur polynomials in n variables are a linear basis for the space of homogeneous degree d symmetric polynomials in n variables.
The first Giambelli formula gives explicit expression of Schur polynomials as a polynomial in the complete homogeneous symmetric polynomials:
The second Giambelli formula gives explicit expression of Schur polynomials as polynomials in the elementary symmetric polynomials:
where  is a dual partition to
is a dual partition to 
These two formulas are also known as "determinantal formulas" and the first one is known as the Jacobi-Trudy identity.
For a partition  , the Schur function is a sum of monomials:
, the Schur function is a sum of monomials:
where the summation is over all semistandard Young tableaux  of shape
of shape  ; the exponents
; the exponents 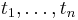 give the weight of
give the weight of  , in other words each
, in other words each 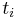 counts the occurrences of the number
counts the occurrences of the number  in
in  . This can be shown to be equivalent to the definition from the first Giambelli formula using the Lindström–Gessel–Viennot lemma (as outlined on that page).
. This can be shown to be equivalent to the definition from the first Giambelli formula using the Lindström–Gessel–Viennot lemma (as outlined on that page).
Schur polynomials sλ can be expressed as linear combinations of monomial symmetric functions mμ with non-negative integer coefficients Kλμ called Kostka numbers:
Example
The following extended example should help clarify these ideas. Consider the case n = 3, d = 4. Using Ferrers diagrams or some other method, we find that there are just four partitions of 4 into at most three parts. We have
and so forth. Summarizing:
Every homogeneous degree-four symmetric polynomial in three variables can be expressed as a unique linear combination of these four Schur polynomials, and this combination can again be found using a Gröbner basis for an appropriate elimination order. For example,
is obviously a symmetric polynomial which is homogeneous of degree four, and we have
Relation to representation theory
The Schur polynomials occur in the representation theory of the symmetric groups, general linear groups, and unitary groups, and in fact this is how they arose. The Weyl character formula implies that the Schur polynomials are the characters of finite dimensional irreducible representations of the general linear groups, and helps to generalize Schur's work to other compact and semisimple Lie groups.
Several expressions arise for this relation, one of the most important being the expansion of the Schur functions 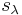 in terms of the symmetric power functions
in terms of the symmetric power functions 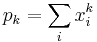 . If we write
. If we write 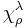 for the character of the representation of the symmetric group indexed by the partition
for the character of the representation of the symmetric group indexed by the partition  evaluated at elements of cycle type indexed by the partition
evaluated at elements of cycle type indexed by the partition  , then
, then
where 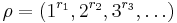 means that the partition
means that the partition  has
has 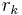 parts of length
parts of length  .
.
Skew Schur functions
Skew Schur functions sλ/μ depend on two partitions λ and μ, and can be defined by the property
See also
- Schubert polynomials. a generalization of Schur polynomials
References
- Macdonald, I. G. (1995). Symmetric functions and Hall polynomials. Oxford Mathematical Monographs (2nd ed.). The Clarendon Press Oxford University Press. ISBN 978-0-19-853489-1. MR1354144. http://www.oup.com/uk/catalogue/?ci=9780198504504
- Sagan, Bruce E. (2001), "Schur functions in algebraic combinatorics", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=s/s120040
- Sturmfels, Bernd (1993). Algorithms in Invariant Theory. New York: Springer. ISBN 0-387-82445-6.
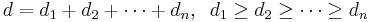
![a_{(d_1, d_2, \dots , d_n)} (x_1, x_2, \dots , x_n) =
\det \left[ \begin{matrix} x_1^{d_1} & x_2^{d_1} & \dots & x_n^{d_1} \\
x_1^{d_2} & x_2^{d_2} & \dots & x_n^{d_2} \\
\vdots & \vdots & \ddots & \vdots \\
x_1^{d_n} & x_2^{d_n} & \dots & x_n^{d_n} \end{matrix} \right]
=\sum_{\sigma\in S_n}\epsilon(\sigma)x_{\sigma(1)}^{d_1}\cdots x_{\sigma(n)}^{d_n}](/2012-wikipedia_en_all_nopic_01_2012/I/fb894d3cd52ba56dd2240b1d219adc29.png)
![a_{(n-1, n-2, \dots , 0)} (x_1, x_2, \dots , x_n) = \det \left[ \begin{matrix} x_1^{n-1} & x_2^{n-1} & \dots & x_n^{n-1} \\
x_1^{n-2} & x_2^{n-2} & \dots & x_n^{n-2} \\
\vdots & \vdots & \ddots & \vdots \\
1 & 1 & \dots & 1 \end{matrix} \right] = \prod_{1 \leq j < k \leq n} (x_j-x_k).](/2012-wikipedia_en_all_nopic_01_2012/I/f60590baa165de2197c288f77fbd9e82.png)
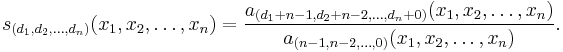
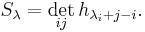
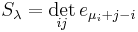
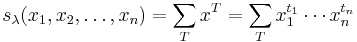
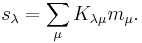
![s_{(2,1,1)} (x_1, x_2, x_3) = \frac{1}{\Delta} \;
\det \left[ \begin{matrix} x_1^4 & x_2^4 & x_3^4 \\ x_1^2 & x_2^2 & x_3^2 \\ x_1 & x_2 & x_3 \end{matrix}
\right] = x_1 \, x_2 \, x_3 \, (x_1 %2B x_2 %2B x_3)](/2012-wikipedia_en_all_nopic_01_2012/I/a817b859e59adc8c4809afaf3ef582a4.png)
![s_{(2,2,0)} (x_1, x_2, x_3) = \frac{1}{\Delta} \;
\det \left[ \begin{matrix} x_1^4 & x_2^4 & x_3^4 \\ x_1^3 & x_2^3 & x_3^3 \\ 1 & 1 & 1 \end{matrix}
\right]= x_1^2 \, x_2^2 %2B x_1^2 \, x_3^2 %2B x_2^2 \, x_3^2
%2B x_1^2 \, x_2 \, x_3 %2B x_1 \, x_2^2 \, x_3 %2B x_1 \, x_2 \, x_3^2](/2012-wikipedia_en_all_nopic_01_2012/I/7e209a9f378b764c8a1c42f837578c63.png)